在本系列的 上一篇文章 中，我们进一步讨论了矩阵和线性代数，并学习了用 JupyterLab 来运行 Python 代码。在本系列的第四篇文章中，我们将开始学习 TensorFlow，这是一个非常强大的人工智能和机器学习库。我们也会简要介绍一些其它有用的库。稍后，我们将讨论概率、理论以及代码。和往常一样，我们先讨论一些能拓宽我们对人工智能的理解的话题。

到目前为止，我们只是从技术方面讨论人工智能。随着越来越多的人工智能产品投入使用，现在是时候分析人工智能的社会影响了。想象一个找工作的场景，如果你的求职申请由人来处理，在申请被拒绝时，你可以从他们那里得到反馈，比如被拒的理由。如果你的求职申请由人工智能程序处理，当你的申请被拒绝时，你不能要求该人工智能软件系统提供反馈。在这种情况下，你甚至不能确定你的申请被拒绝是否确实是仅基于事实的决定。这明确地告诉我们，从长远来看，我们需要的不仅仅是魔法般的结果，还需要人工智能具有 责任 accountability 和 保证 guarantee 。（LCTT 译注：责任主要指确保系统的决策过程是透明的、可解释的，并且对系统的行为负责。保证是指对于系统性能指标和行为的一种承诺或者预期。）目前有很多试图回答这些问题的研究。

人工智能的应用也会引发许多道德和伦理上的问题。我们不必等到强人工智能（也被称为 通用人工智能 artificial general intelligence —— AGI）出现才研究它的社会影响。我们可以通过思想实验来探究人工智能的影响。想象你在一个雨夜你驾车行驶在有发夹完的道路上，突然你眼前有人横穿马路，你的反应是什么？如果你突然刹车或转向，你自己的生命将处于极大的危险之中。但如果你不这样做，过马路的人恐怕凶多吉少。因为我们人类具有自我牺牲的特质，在决策的瞬间，即使是最自私的人也可能决定救行人。但我们如何教会人工智能系统模仿这种行为呢？毕竟从纯粹的逻辑来看，自我牺牲是一个非常糟糕的选择。

同样的场景下，如果汽车是由人工智能软件在驾驶会发生什么呢？既然你是汽车的主人，那么人工智能软件理应把你的安全放在首位，它甚至全不顾其他乘客的安全。很容易看出，如果世界上所有的汽车都由这样的软件控制的话将导致彻底的混乱。现在，如果进一步假设乘坐自动驾驶汽车的乘客身患绝症。那么对于一个数学机器来说，为了行人牺牲乘客是合乎逻辑的。但对于我们这些有血有肉的人却不见得如此。你可以花点时间思考一下其它场景，注重逻辑的机器和热血的人类都会做出什么样的决策。

有很多书籍和文章在讨论人工智能全面运作后的政治、社会和伦理方面的问题。但对于我们这些普通人和计算机工程师来说，读所有的书都是不必要的。然而，由于人工智能的社会意义如此重要，我们也不能轻易搁置这个问题。为了了解人工智能的社会政治方面，我建议你通过几部电影来理解人工智能（强人工智能）如何影响我们所有人。 斯坦利·库布里克 Stanley Kubrick 的杰作《 2001：太空漫游 2001: A Space Odyssey 》是最早描绘超级智能生物如何俯视我们人类的电影之一。这部电影中人工智能认为人类是世界最大的威胁，并决定毁灭人类。事实上，有相当多的电影都在探索这种情节。由伟大的艺术大师 史蒂文·斯皮尔伯格 Steven Spielberg 亲自执导的《 人工智能 Artificial Intelligence 》，探讨了人工智能机器如何与人类互动。另一部名为《 机械姬 Ex Machina 》的电影详细阐述了这一思路，讲述了具有人工智能的机器。在我看来这些都是了解人工智能的影响必看的电影。

最后思考一下，试想如果马路上的汽车使用来自制造商的不同的自动驾驶规则和人工智能，这将导致彻底的混乱。

TensorFlow 入门

TensorFlow 是由 谷歌大脑 Google Brain 团队开发的一个自由开源的库，使用 Apache 2.0 许可证。TensorFlow 是开发人工智能和机器学习程序的重量级的库。除了 Python 之外，TensorFlow 还提供 C++、Java、JavaScript 等编程语言的接口。在我们进一步讨论之前，有必要解释一下 张量 tensor 是什么。如果你熟悉物理学，张量这个词对你来说可能并不陌生。但如果你不知道张量是什么也不用担心，现阶段把它看作多维数组就行了。当然，这是一种过度简化的理解。TensorFlow 可以在 NumPy 提供的多维数组之上运行。

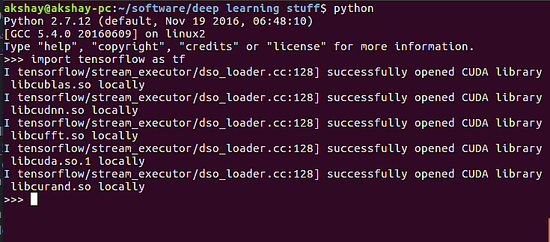
首先，我们要在 JupyterLab 中安装 TensorFlow。TensorFlow 有 GPU 版本和 CPU 版本两种安装类型可以选择。这主要取决于你的系统是否有合适的 GPU。GPU 是一种利用并行处理来加快图像处理速度的电路。它被广泛用在游戏和设计领域，在开发人工智能和机器学习程序时也是必不可少的硬件。但一个不太好的消息是 TensorFlow 只兼容英伟达的 GPU。此外，你需要在系统中安装一个称为 CUDA（ 计算统一设备架构 compute unified device architecture ）的并行计算平台。如果你的系统满足这些要求，那么在 JupyterLab 上执行命令 pip install tensorflow-gpu 来安装 GPU 版本的 TensorFlow。如果你系统的 GPU 配置无法满足要求，当你尝试使用 TensorFlow 时，会得到如下错误消息：“CUDA\_ERROR\_NO\_DEVICE: no CUDA-capable device is detected”。此时使用 pip uninstall tensorflow-gpu 卸载 GPU 版本的 TensorFlow。然后执行命令 pip install tensorflow 安装 CPU 版本的 TensorFlow。现在 TensorFlow 就准备就绪了。请注意，目前我们将讨论限制在 CPU 和 TensorFlow 上。

现在，让我们运行第一个由 TensorFlow 驱动的 Python 代码。图 1 显示了一个简单的 Python 脚本及其在 JupyterLab 上执行时的输出。前两行代码将库 NumPy 和 TensorFlow 导入到 Python 脚本中。顺便一提，如果你想在 Jupyter Notebook 单元中显示行号，单击菜单 “ 查看 View > 显示行号 Show Line Numbers ”。第 3 行使用 NumPy 创建了一个名为 arr 的数组，其中包含三个元素。第 4 行代码将数组 arr 的每个元素乘 3，将结果存储在一个名为 ten 的变量中。第 5 行和第 6 行分别打印变量 arr 和 ten 的类型。从代码的输出中可以看到，arr 和 ten 的类型是不同的。第 7 行打印变量 ten 的值。注意，ten 的形状与数组 arr 的形状是相同的。 数据类型 int64 在本例中用于表示整数。这使得本例中 NumPy 和 TensorFlow 数据类型之间的无缝转换成为可能。

TensorFlow 支持很多操作和运算。随着处理的数据量的增加，这些操作会变得越来越复杂。TensorFlow 支持常见的算术运算，比如乘法、减法、除法、幂运算、模运算等。如果参与运算的是列表或元组，TensorFlow 会逐元素执行该操作。

TensorFlow 还支持逻辑运算、关系运算和位运算。这里的操作也是按元素执行的。图 2 显示了执行这些按元素操作的 Python 脚本。第 1 行代码从列表创建一个张量，并将其存储在变量 t1 中。TensorFlow 的函数 constant() 用于从 Python 对象（如列表、元组等）创建张量。类似地，第 2 行创建了另一个张量 t2。第 3 行和第 4 行都是执行逐元素求幂并打印输出。从图 2 中可以清楚地看出，该求幂的结果是相同的。第 5 行代码比较张量 t1 和 t2 的元素并打印结果。输出中的 [True True False] 分别是对应 3>2、4>3 和 2>6 的结果。第 6 行的输出与之类似。

图 3 展示了 TensorFlow 处理矩阵的例子。第 1 行和第 3 行分别构造两个矩阵 x 和 y，第 2 行和第 4 行分别打印矩阵 x 和 y的形状。代码的输出显示 x 的形状为 (3,3)，y 的形状为 (3，)。从本系列前面介绍的矩阵知识，我们知道这两个矩阵是不能相乘的。

因此，在第 5 行中将矩阵 y 增加了一个维度。在第 6 行，再次打印矩阵 y 的形状，输出结果为 (3,1)。现在矩阵 x 和 y 可以相乘了。第 7 行中，将矩阵相乘并打印输出。注意，类似的操作也可以在张量上执行，即使张量的维数很高，TensorFlow 也可以很好地扩展。在本系列的后续文章中，我们将更多地了解 TensorFlow 支持的数据类型和其他复杂操作。

既然介绍了 TensorFlow，我想我也应该提一下 Keras。它为 TensorFlow 提供 Python 接口。在后续的文章中，我们将专门介绍 Keras。

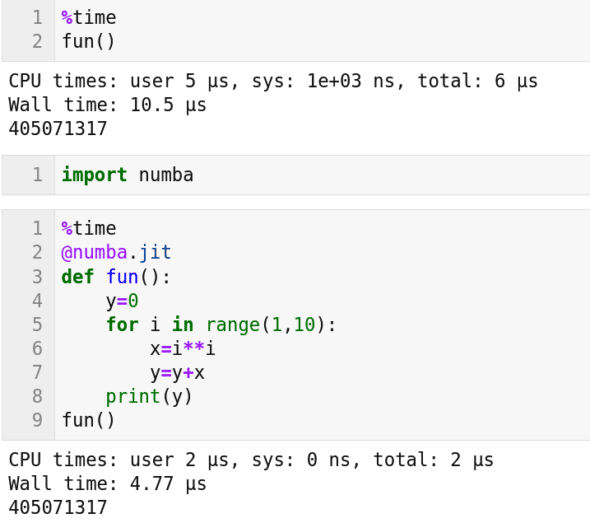
我们如何利用非英伟达 GPU 的能力呢？有许多功能强大的软件包可以做到这一点。比如 PyOpenCL，一个在 Python 中编写并行程序的框架。它让我们可以使用 OpenCL（ 开放计算语言 open computing language ）。OpenCL 可以与 AMD、Arm、英伟达等厂商的 GPU 进行交互。当然还有其他选择，比如 Numba。它是一种JIT 编译器，可用在代码执行期间将 Python 代码编译为机器码。如果 GPU 可用，Numba 允许代码使用的 GPU 能力。图 4 是展示了使用 Numba 的 Python 代码。

我们可以看到函数 fun() 具有允许并行化的特征。从图 4 中可以看到，代码在不使用和使用 Numba 的情况下的答案是相同的。但是我们可以看到所花费的执行时间是不同的。当使用 Numba 并行化代码时，只花费了不到一半的时间。此外随着问题规模的增加，并行化和非并行化版本所花费的时间之间的差距也将增加。

SymPy 入门

SymPy 是一个用于符号计算的 Python 库。通过图 5 中的例子，让我们试着理解什么是符号计算。它使用 SymPy 提供的函数 Integral()来求积分。图 5 也显示了这个符号计算的输出。注意，SciPy 提供的 integrate() 函数返回数值计算结果，而 SymPy 的 Integral() 函数能提供精确的符号结果表达式。人工智能和机器学习程序开发中会用到一些统计学操作，SymPy 在执行这些操作时非常有用。

在本系列的下一篇文章中，我们将讨论 Theano。Theano 是一个 Python 库和优化编译器，用于计算数学表达式。

概率论入门

现在是概率论出场的时候了，它是人工智能和机器学习的另一个重要话题。对概率论的详细讨论超出了本系列的范围。我强烈建议在继续阅读之前，先通过维基百科上关于“概率”、“贝叶斯定理”和“标准差”的文章了解一些重要的术语和概念，如概率、独立事件、互斥事件、条件概率、贝叶斯定理、均值、标准差等。学习完这些后，你将能够轻松理解后面关于概率的讨论。

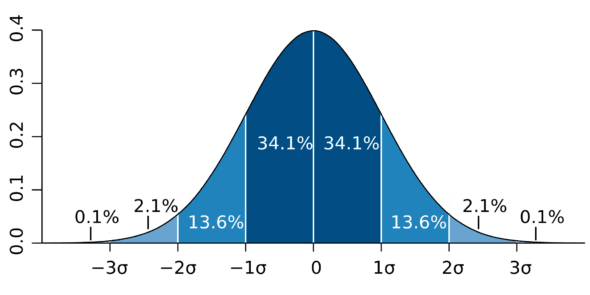
我们从概率分布开始讲起。根据维基百科的说法，“概率分布是一个数学函数，它能给出一个实验中不同的可能结果发生的概率”。现在，让我们试着理解什么是概率分布函数。最著名的概率分布函数是正态分布，通常也称为高斯分布（以伟大的数学家高斯的名字命名）。正态分布函数的图像是一条钟形曲线。图 6 是一个钟形曲线的例子。钟形曲线的确切形状取决于均值和标准差。让我们试着通过分析一种自然现象来理解钟形曲线。从网上可以查到，中国男性的平均身高约为1.7米。在我们周围的到多数男性的身高都非常接近这个数字。你看到一个身高低于1.4米或高于2米的男人的可能性很小。如果记录 100 万人的身高，然后以横轴为身高，纵轴为该身高的人数，绘制统计结果，你会发现绘制出的图像近似为钟形曲线，其中只有一些轻微的倾斜和弯曲。因此，正态分布很容易地捕捉到自然现象的概率特征。

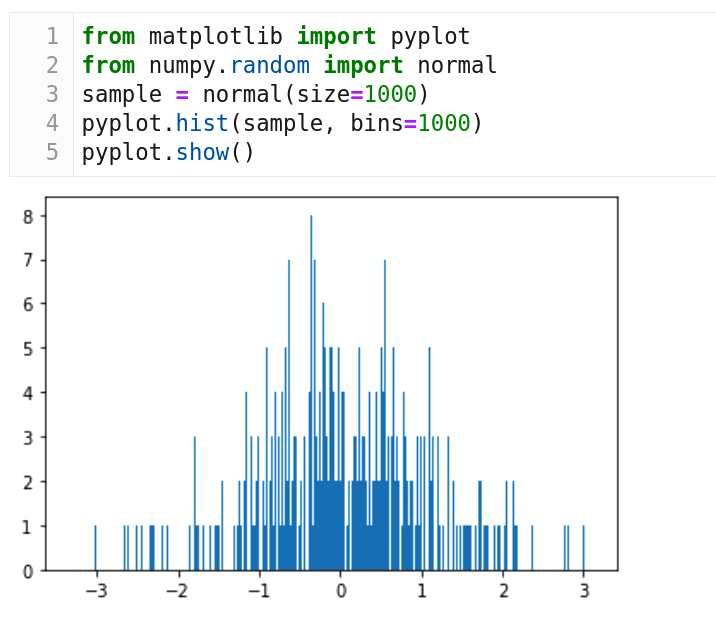
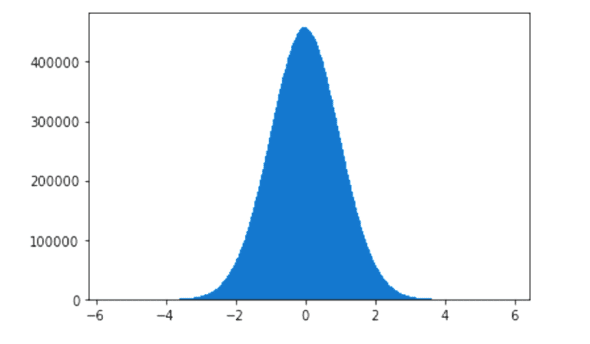
现在，我们来看一个使用正态分布的例子。图 7 的代码中我们使用 NumPy 的正态分布的函数 normal()，然后使用 Matplotlib 进行绘图。从第 3 行我们可以看到样本大小为 1000。第 4 行绘制一个包含 1000 个 桶 bin 的直方图。但是图 7 的钟形曲线与图 6 中看到的钟形曲线相差很大。究其原因是我们的样本数量只有 1000。样本量应该足够大才能获得更清晰的图像。将第 3 行代码替换为 sample = normal(size=100000000)，行并再次执行程序。图 8 显示了一条更好的钟形曲线。这一次，我们的样本大小为 100,000,000，钟形曲线与图 6 所示非常相似。正态分布和钟形曲线只是开始。在下一篇文章中，我们将讨论可以概括其他事件和自然现象的概率分布函数。下一次，我们还将更正式地讨论这个主题。

本篇的内容就到此结束了。在下一篇文章中，我们将继续探索概率和统计中的一些概念。我们还将安装和使用 Anaconda，这是一个用于科学计算的 Python 发行版，对于开发人工智能、机器学习和数据科学程序特别有用。如前所述，我们还将熟悉另一个名为 Theano 的 Python 库，它在人工智能和机器学习领域被大量使用。

（题图：DA/2a8d805a-01d3-4039-b96c-74766491e264）

via: https://www.opensourceforu.com/2023/01/ai-an-introduction-to-probability/

作者：Deepu Benson 选题：lujun9972 译者：toknow-gh 校对：wxy

本文由 LCTT 原创编译，Linux中国 荣誉推出

有一个令人震惊的事实，即人工智能和机器学习的工具和技术在近期迅速兴起。深度学习，或者说“注射了激素的机器学习”，数据科学家和机器学习专家在这个领域有数不胜数等可用的库和框架。很多这样的框架都是基于 Python 的，因为 Python 是一个更通用，相对简单的语言。Theano、Keras、 TensorFlow 是几个基于 Python 构建的流行的深度学习库，目的是使机器学习专家更轻松。

Google 的 TensorFlow 是一个被广泛使用的机器学习和深度学习框架。 TensorFlow 开源于 2015 年，得到了机器学习专家社区的广泛支持，TensorFlow 已经迅速成长为许多机构根据其机器学习和深度学习等需求而选择的框架。 另一方面，PyTorch 是由 Facebook 最近开发的用于训练神经网络的 Python 包，改编自基于 Lua 的深度学习库 Torch。 PyTorch 是少数可用的深度学习框架之一，它使用 基于磁带的自动梯度系统 tape-based autograd system ，以快速和灵活的方式构建动态神经网络。

在这篇文章中，我们将 PyTorch 与 TensorFlow 进行不同方面的比较。

让我们开始吧！

什么编程语言支持 PyTorch 和 TensorFlow？

虽然主要是用 C++ 和 CUDA 编写的，但 TensorFlow 包含一个位于核心引擎上的 Python API，使得更便于被 Python 支持者 Pythonistas 使用。 除了 Python，它还包括 C++、Haskell、Java、Go 和 Rust 等其他 API，这意味着开发人员可以用他们的首选语言进行编码。

虽然 PyTorch 是一个 Python 软件包，但你也可以提供使用基本的 C/C++ 语言的 API 进行编码。 如果你习惯使用 Lua 编程语言，你也可以使用 Torch API 在 PyTorch 中编写神经网络模型。

PyTorch 和 TensorFlow 有多么易于使用？

如果将 TensorFlow 作为一个独立的框架使用，它可能会有点复杂，并且会给深度学习模型的训练带来一些困难。 为了减少这种复杂性，可以使用位于 TensorFlow 复杂引擎之上的 Keras 封装，以简化深度学习模型的开发和训练。 TensorFlow 也支持 PyTorch 目前没有的分布式培训。 由于包含 Python API，TensorFlow 也可以在生产环境中使用，即可用于培训练和部署企业级深度学习模型。

PyTorch 由于 Torch 的复杂用 Python 重写。 这使得 PyTorch 对于开发人员更为原生。 它有一个易于使用的框架，提供最大化的灵活和速度。 它还允许在训练过程中快速更改代码而不妨碍其性能。 如果你已经有了一些深度学习的经验，并且以前使用过 Torch，那么基于它的速度、效率和易用性，你会更喜欢 PyTorch。 PyTorch 包含定制的 GPU 分配器，这使得深度学习模型具有更高的内存效率。 由此，训练大型深度学习模型变得更容易。 因此，Pytorch 在 Facebook、Twitter、Salesforce 等大型组织广受欢迎。

用 PyTorch 和 TensorFlow 训练深度学习模型

PyTorch 和 TensorFlow 都可以用来建立和训练神经网络模型。

TensorFlow 工作于 SCG（静态计算图）上，包括在模型开始执行之前定义静态图。 但是，一旦开始执行，在模型内的调整更改的唯一方法是使用 tf.session 和 tf.placeholder 张量。

PyTorch 非常适合训练 RNN（递归神经网络），因为它们在 PyTorch 中比在 TensorFlow 中运行得更快。 它适用于 DCG（动态计算图），可以随时在模型中定义和更改。 在 DCG 中，每个模块可以单独调试，这使得神经网络的训练更简单。

TensorFlow 最近提出了 TensorFlow Fold，这是一个旨在创建 TensorFlow 模型的库，用于处理结构化数据。 像 PyTorch 一样，它实现了 DCG，在 CPU 上提供高达 10 倍的计算速度，在 GPU 上提供超过 100 倍的计算速度！ 在 Dynamic Batching 的帮助下，你现在可以执行尺寸和结构都不相同的深度学习模型。

GPU 和 CPU 优化的比较

TensorFlow 的编译时间比 PyTorch 短，为构建真实世界的应用程序提供了灵活性。 它可以从 CPU、GPU、TPU、移动设备到 Raspberry Pi（物联网设备）等各种处理器上运行。

另一方面，PyTorch 包括 张量 tensor 计算，可以使用 GPU 将深度神经网络模型加速到 50 倍或更多。 这些张量可以停留在 CPU 或 GPU 上。 CPU 和 GPU 都是独立的库， 无论神经网络大小如何，PyTorch 都可以高效地利用。

社区支持

TensorFlow 是当今最流行的深度学习框架之一，由此也给它带来了庞大的社区支持。 它有很好的文档和一套详细的在线教程。 TensorFlow 还包括许多预先训练过的模型，这些模型托管和提供于 GitHub。 这些模型提供给热衷于使用 TensorFlow 开发者和研究人员一些现成的材料来节省他们的时间和精力。

另一方面，PyTorch 的社区相对较小，因为它最近才发展起来。 与 TensorFlow 相比，文档并不是很好，代码也不是很容易获得。 然而，PyTorch 确实允许个人与他人分享他们的预训练模型。

PyTorch 和 TensorFlow —— 力量悬殊的故事

就目前而言，由于各种原因，TensorFlow 显然比 PyTorch 更受青睐。

TensorFlow 很大，经验丰富，最适合实际应用。 是大多数机器学习和深度学习专家明显的选择，因为它提供了大量的功能，最重要的是它在市场上的成熟应用。 它具有更好的社区支持以及多语言 API 可用。 它有一个很好的文档库，由于从准备到使用的代码使之易于生产。 因此，它更适合想要开始深度学习的人，或者希望开发深度学习模型的组织。

虽然 PyTorch 相对较新，社区较小，但它速度快，效率高。 总之，它给你所有的优势在于 Python 的有用性和易用性。 由于其效率和速度，对于基于研究的小型项目来说，这是一个很好的选择。 如前所述，Facebook、Twitter 等公司正在使用 PyTorch 来训练深度学习模型。 但是，使用它尚未成为主流。 PyTorch 的潜力是显而易见的，但它还没有准备好去挑战这个 TensorFlow 野兽。 然而，考虑到它的增长，PyTorch 进一步优化并提供更多功能的日子并不遥远，直到与 TensorFlow可以 比较。

作者： Savia Lobo，非常喜欢数据科学。 喜欢更新世界各地的科技事件。 喜欢歌唱和创作歌曲。 相信才智上的艺术。

via: https://datahub.packtpub.com/deep-learning/dl-wars-pytorch-vs-tensorflow/

作者：Savia Lobo 译者：Wuod3n 校对：wxy

本文由 LCTT 原创编译，Linux中国 荣誉推出

在本文中，我们将看一些 TensorFlow 的例子，并从中感受到在定义 张量 tensor 和使用张量做数学计算方面有多么容易，我还会举些别的机器学习相关的例子。

TensorFlow 是什么?

TensorFlow 是 Google 为了解决复杂的数学计算耗时过久的问题而开发的一个库。

事实上，TensorFlow 能干许多事。比如：

• 求解复杂数学表达式
• 机器学习技术。你往其中输入一组数据样本用以训练，接着给出另一组数据样本基于训练的数据而预测结果。这就是人工智能了！
• 支持 GPU 。你可以使用 GPU（图像处理单元）替代 CPU 以更快的运算。TensorFlow 有两个版本： CPU 版本和 GPU 版本。

开始写例子前，需要了解一些基本知识。

什么是张量？

张量 tensor 是 TensorFlow 使用的主要的数据块，它类似于变量，TensorFlow 使用它来处理数据。张量拥有维度和类型的属性。

维度指张量的行和列数，读到后面你就知道了，我们可以定义一维张量、二维张量和三维张量。

类型指张量元素的数据类型。

定义一维张量

可以这样来定义一个张量：创建一个 NumPy 数组（LCTT 译注：NumPy 系统是 Python 的一种开源数字扩展，包含一个强大的 N 维数组对象 Array，用来存储和处理大型矩阵 ）或者一个 Python 列表 ，然后使用 tf_convert_to_tensor 函数将其转化成张量。

可以像下面这样，使用 NumPy 创建一个数组：

import numpy as np arr = np.array([1, 5.5, 3, 15, 20])
arr = np.array([1, 5.5, 3, 15, 20])

运行结果显示了这个数组的维度和形状。

import numpy as np
arr = np.array([1, 5.5, 3, 15, 20])
print(arr)
print(arr.ndim)
print(arr.shape)
print(arr.dtype)

它和 Python 列表很像，但是在这里，元素之间没有逗号。

现在使用 tf_convert_to_tensor 函数把这个数组转化为张量。

import numpy as np
import tensorflow as tf
arr = np.array([1, 5.5, 3, 15, 20])
tensor = tf.convert_to_tensor(arr,tf.float64)
print(tensor)

这次的运行结果显示了张量具体的含义，但是不会展示出张量元素。

要想看到张量元素，需要像下面这样，运行一个会话：

import numpy as np
import tensorflow as tf
arr = np.array([1, 5.5, 3, 15, 20])
tensor = tf.convert_to_tensor(arr,tf.float64)
sess = tf.Session()
print(sess.run(tensor))
print(sess.run(tensor[1]))

定义二维张量

定义二维张量，其方法和定义一维张量是一样的，但要这样来定义数组：

arr = np.array([(1, 5.5, 3, 15, 20),(10, 20, 30, 40, 50), (60, 70, 80, 90, 100)])

接着转化为张量：

import numpy as np
import tensorflow as tf
arr = np.array([(1, 5.5, 3, 15, 20),(10, 20, 30, 40, 50), (60, 70, 80, 90, 100)])
tensor = tf.convert_to_tensor(arr)
sess = tf.Session()
print(sess.run(tensor))

现在你应该知道怎么定义张量了，那么，怎么在张量之间跑数学运算呢？

在张量上进行数学运算

假设我们有以下两个数组：

arr1 = np.array([(1,2,3),(4,5,6)])
arr2 = np.array([(7,8,9),(10,11,12)])

利用 TenserFlow ，你能做许多数学运算。现在我们需要对这两个数组求和。

使用加法函数来求和：

import numpy as np
import tensorflow as tf
arr1 = np.array([(1,2,3),(4,5,6)])
arr2 = np.array([(7,8,9),(10,11,12)])
arr3 = tf.add(arr1,arr2)
sess = tf.Session()
tensor = sess.run(arr3)
print(tensor)

也可以把数组相乘：

import numpy as np
import tensorflow as tf
arr1 = np.array([(1,2,3),(4,5,6)])
arr2 = np.array([(7,8,9),(10,11,12)])
arr3 = tf.multiply(arr1,arr2)
sess = tf.Session()
tensor = sess.run(arr3)
print(tensor)

现在你知道了吧。

三维张量

我们已经知道了怎么使用一维张量和二维张量，现在，来看一下三维张量吧，不过这次我们不用数字了，而是用一张 RGB 图片。在这张图片上，每一块像素都由 x、y、z 组合表示。

这些组合形成了图片的宽度、高度以及颜色深度。

首先使用 matplotlib 库导入一张图片。如果你的系统中没有 matplotlib ，可以 使用 pip来安装它。

将图片放在 Python 文件的同一目录下，接着使用 matplotlib 导入图片：

import matplotlib.image as img
myfile = "likegeeks.png"
myimage = img.imread(myfile)
print(myimage.ndim)
print(myimage.shape)

从运行结果中，你应该能看到，这张三维图片的宽为 150 、高为 150 、颜色深度为 3 。

你还可以查看这张图片：

import matplotlib.image as img
import matplotlib.pyplot as plot
myfile = "likegeeks.png"
myimage = img.imread(myfile)
plot.imshow(myimage)
plot.show()

真酷！

那怎么使用 TensorFlow 处理图片呢？超级容易。

使用 TensorFlow 生成或裁剪图片

首先，向一个占位符赋值：

myimage = tf.placeholder("int32",[None,None,3])

使用裁剪操作来裁剪图像：

cropped = tf.slice(myimage,[10,0,0],[16,-1,-1])

最后，运行这个会话：

result = sess.run(cropped, feed\_dict={slice: myimage})

然后，你就能看到使用 matplotlib 处理过的图像了。

这是整段代码：

import tensorflow as tf
import matplotlib.image as img
import matplotlib.pyplot as plot
myfile = "likegeeks.png"
myimage = img.imread(myfile)
slice = tf.placeholder("int32",[None,None,3])
cropped = tf.slice(myimage,[10,0,0],[16,-1,-1])
sess = tf.Session()
result = sess.run(cropped, feed_dict={slice: myimage})
plot.imshow(result)
plot.show()

是不是很神奇？

使用 TensorFlow 改变图像

在本例中，我们会使用 TensorFlow 做一下简单的转换。

首先，指定待处理的图像，并初始化 TensorFlow 变量值：

myfile = "likegeeks.png"
myimage = img.imread(myfile)
image = tf.Variable(myimage,name='image')
vars = tf.global_variables_initializer()

然后调用 transpose 函数转换，这个函数用来翻转输入网格的 0 轴和 1 轴。

sess = tf.Session()
flipped = tf.transpose(image, perm=[1,0,2])
sess.run(vars)
result=sess.run(flipped)

接着你就能看到使用 matplotlib 处理过的图像了。

import tensorflow as tf
import matplotlib.image as img
import matplotlib.pyplot as plot
myfile = "likegeeks.png"
myimage = img.imread(myfile)
image = tf.Variable(myimage,name='image')
vars = tf.global_variables_initializer()
sess = tf.Session()
flipped = tf.transpose(image, perm=[1,0,2])
sess.run(vars)
result=sess.run(flipped)
plot.imshow(result)
plot.show()

以上例子都向你表明了使用 TensorFlow 有多么容易。

via: https://www.codementor.io/likegeeks/define-and-use-tensors-using-simple-tensorflow-examples-ggdgwoy4u

作者：LikeGeeks 译者：ghsgz 校对：wxy

本文由 LCTT 原创编译，Linux中国 荣誉推出

TensorFlow 是用于机器学习任务的开源软件。它的创建者 Google 希望提供一个强大的工具以帮助开发者探索和建立基于机器学习的应用，所以他们在去年作为开源项目发布了它。TensorFlow 是一个非常强大的工具，专注于一种称为 深层神经网络 deep neural network （DNN）的神经网络。

深层神经网络被用来执行复杂的机器学习任务，例如图像识别、手写识别、自然语言处理、聊天机器人等等。这些神经网络被训练学习其所要执行的任务。由于训练所需的计算是非常巨大的，在大多数情况下需要 GPU 支持，这时 TensorFlow 就派上用场了。启用了 GPU 并安装了支持 GPU 的软件，那么训练所需的时间就可以大大减少。

本教程可以帮助你安装只支持 CPU 的和同时支持 GPU 的 TensorFlow。要使用带有 GPU 支持的 TensorFLow，你必须要有一块支持 CUDA 的 Nvidia GPU。CUDA 和 CuDNN（Nvidia 的计算库）的安装有点棘手，本指南会提供在实际安装 TensorFlow 之前一步步安装它们的方法。

Nvidia CUDA 是一个 GPU 加速库，它已经为标准神经网络中用到的标准例程调优过。CuDNN 是一个用于 GPU 的调优库，它负责 GPU 性能的自动调整。TensorFlow 同时依赖这两者用于训练并运行深层神经网络，因此它们必须在 TensorFlow 之前安装。

需要指出的是，那些不希望安装支持 GPU 的 TensorFlow 的人，你可以跳过以下所有的步骤并直接跳到：“步骤 5：安装只支持 CPU 的 TensorFlow”。

关于 TensorFlow 的介绍可以在这里找到。

1、 安装 CUDA

首先，在这里下载用于 Ubuntu 16.04 的 CUDA 库。此文件非常大（2GB），因此也许会花费一些时间下载。

下载的文件是 “.deb” 包。要安装它，运行下面的命令：

sudo dpkg -i cuda-repo-ubuntu1604-8-0-local_8.0.44-1_amd64.deb

下面的的命令会安装所有的依赖，并最后安装 cuda 工具包：

sudo apt install -f
sudo apt update
sudo apt install cuda

如果成功安装，你会看到一条消息说：“successfully installed”。如果已经安装了，接着你可以看到类似下面的输出：

2、安装 CuDNN 库

CuDNN 下载需要花费一些功夫。Nvidia 没有直接提供下载文件（虽然它是免费的）。通过下面的步骤获取 CuDNN。

1. 点击此处进入 Nvidia 的注册页面并创建一个帐户。第一页要求你输入你的个人资料，第二页会要求你回答几个调查问题。如果你不知道所有答案也没问题，你可以随便选择一个选项。
2. 通过前面的步骤，Nvidia 会向你的邮箱发送一个激活链接。在你激活之后，直接进入这里的 CuDNN 下载链接。
3. 登录之后，你需要填写另外一份类似的调查。随机勾选复选框，然后点击调查底部的 “proceed to Download”，在下一页我们点击同意使用条款。

4. 最后，在下拉中点击 “Download cuDNN v5.1 (Jan 20, 2017), for CUDA 8.0”，最后，你需要下载这两个文件：

   • cuDNN v5.1 Runtime Library for Ubuntu14.04 (Deb)
   • cuDNN v5.1 Developer Library for Ubuntu14.04 (Deb)

注意：即使上面说的是用于 Ubuntu 14.04 的库。它也适用于 16.04。

现在你已经同时有 CuDNN 的两个文件了，是时候安装它们了！在包含这些文件的文件夹内运行下面的命令：

sudo dpkg -i libcudnn5_5.1.5-1+cuda8.0_amd64.deb
sudo dpkg -i libcudnn5-dev_5.1.5-1+cuda8.0_amd64.deb

下面的图片展示了这些命令的输出：

3、 在 bashrc 中添加安装位置

安装位置应该被添加到 bashrc 文件中，以便系统下一次知道如何找到这些用于 CUDA 的文件。使用下面的命令打开 bashrc 文件：

sudo gedit ~/.bashrc

文件打开后，添加下面两行到文件的末尾：

export LD_LIBRARY_PATH="$LD_LIBRARY_PATH:/usr/local/cuda/lib64:/usr/local/cuda/extras/CUPTI/lib64"
export CUDA_HOME=/usr/local/cuda

4、 安装带有 GPU 支持的 TensorFlow

这步我们将安装带有 GPU 支持的 TensorFlow。如果你使用的是 Python 2.7，运行下面的命令：

pip install TensorFlow-gpu

如果安装了 Python 3.x，使用下面的命令：

pip3 install TensorFlow-gpu

安装完后，你会看到一条 “successfully installed” 的消息。现在，剩下要测试的是是否已经正确安装。打开终端并输入下面的命令测试：

python
import TensorFlow as tf

你应该会看到类似下面图片的输出。在图片中你可以观察到 CUDA 库已经成功打开了。如果有任何错误，消息会提示说无法打开 CUDA 甚至无法找到模块。为防你或许遗漏了上面的某步，仔细重做教程的每一步就行了。

5、 安装只支持 CPU 的 TensorFlow

注意：这步是对那些没有 GPU 或者没有 Nvidia GPU 的人而言的。其他人请忽略这步！！

安装只支持 CPU 的 TensorFlow 非常简单。使用下面两个命令：

pip install TensorFlow

如果你有 python 3.x，使用下面的命令：

pip3 install TensorFlow

是的，就是这么简单！

安装指南至此结束，你现在可以开始构建深度学习应用了。如果你刚刚起步，你可以在这里看下适合初学者的官方教程。如果你正在寻找更多的高级教程，你可以在这里学习了解如何设置可以高精度识别上千个物体的图片识别系统/工具。

（题图：Pixabay，CC0）

via: https://www.howtoforge.com/tutorial/installing-tensorflow-neural-network-software-for-cpu-and-gpu-on-ubuntu-16-04/

作者：Akshay Pai 译者：geekpi 校对：wxy

本文由 LCTT 原创编译，Linux中国 荣誉推出