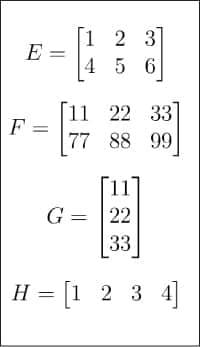人工智能教程(七):Scikit-learn 和训练第一个模型

在本系列的 上一篇文章 中,我们用 TensorFlow 构建了第一个神经网络,然后还通过 Keras 接触了第一个数据集。在本系列的第七篇文章中,我们将继续探索神经网络,并使用数据集来训练模型。我们还将介绍另一个强大的机器学习 Python 库 scikit-learn。不过在进入正题之前,我要介绍两个轰动性的人工智能应用:ChatGPT 和 DALL-E 2。(LCTT 译注:此文原文发表于 2023 年初,恰值以 ChatGPT 为代表的 AI 热潮开始掀起。)
OpenAI 是一个人工智能研究实验室,它在人工智能和机器学习领域做了很多研究。 埃隆·马斯克 是该组织的联合创始人之一。2022 年 11 月,该实验室推出了一款名为 ChatGPT 的在线工具。它是一个可以像人类一样聊天的人工智能聊天机器人。它是使用监督学习和强化学习技术训练的 大型语言模型 (LLM)。ChatGPT 使用了 OpenAI 的 GPT-3.5 语言模型,这是 GPT-3( 生成式预训练变换器 )的改进版本,GPT-3 是一种使用深度学习来生成类似人类文本的语言模型。(LCTT 译注:OpenAI 已于 2023 年 3 月 14 日 发布了 GPT-4.0,它支持图文混合的输入输出,并大幅提升了推理能力和准确性。)我仍然记得第一次使用 ChatGPT 时的兴奋。它清楚地展现了人工智能的能力。ChatGPT 的回答质量很高,通常与人类给出的答案没有区别。你可以使用它来纠正语法错误、改写句子、总结段落、编写程序等。实际上,我就用 ChatGPT 改写了本文中的许多句子。此外,我还故意使用有语法错误的文本测试了 ChatGPT,它纠正后的句子非常准确。它重新措辞和总结段落的能力也很惊人。
程序员甚至有可能使用 ChatGPT 在短时间内解决编程难题。在 编程探险挑战赛 2022 中,就有人这样宣称(LCTT 译注:比赛官方只是没有完全禁止使用人工智能作为辅助,但是并不很推崇这样的作法。消息来源)。事实上在 2022 年 12 月,也就是 ChatGPT 发布的一个月后,Stack Overflow 发布了一条新的规定,禁止提交 GPT 或 ChatGPT 生成答案。(LCTT 译注:消息来源:Temporary policy Generative AI (e.g., ChatGPT) is banned - Meta Stack Overflow)
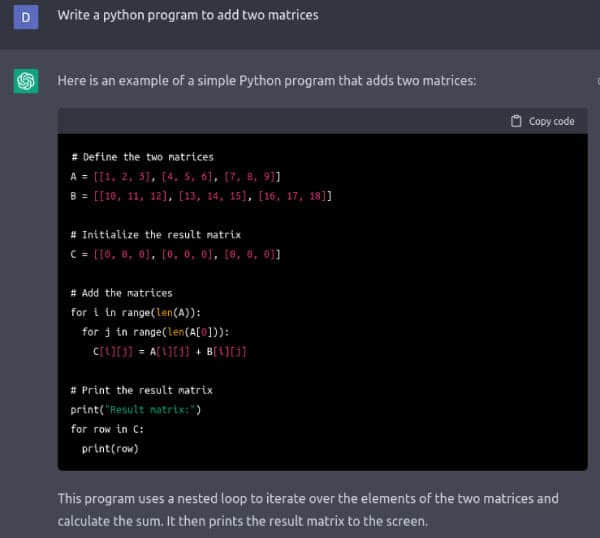
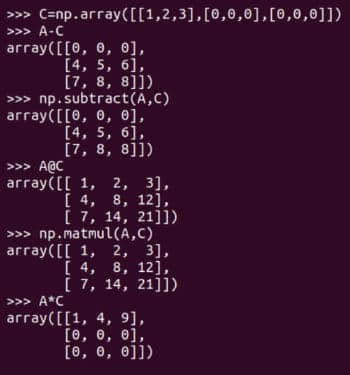
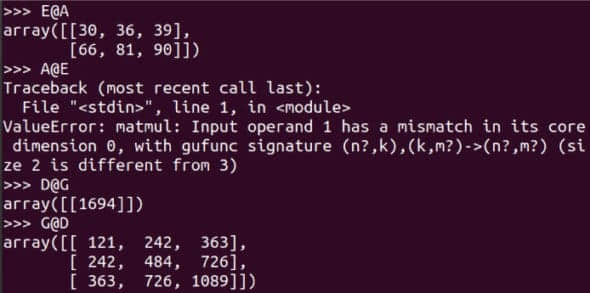
图 1 显示了 ChatGPT 编写的将两个矩阵相加的 Python 程序。我要求用 BASIC、FORTRAN、Pascal、Haskell、Lua、Pawn、C、c++、Java 等语言编写程序,ChatGPT 总能给出答案,甚至对于像 Brainfuck 和 Ook! 这样生僻的编程语言也是如此。我很确定 ChatGPT 没有从互联网上复制程序代码。更确切地说,我认为 ChatGPT 是基于对上述编程语言的语法知识生成了这些答案的,这些知识是从训练它的大量数据中获得的。许多专家和观察人士认为,随着 ChatGPT 的发展,人工智能已经成为主流。ChatGPT 的真正力量将在未来几个月或几年里被看到。
OpenAI 的另一个令人惊叹的在线人工智能工具是 DALL-E 2,它以卡通机器人 WALL-E(LCTT 译注:电源《机器人总动员》中的主角)和著名画家/艺术家 萨尔瓦多·达利 的名字命名。DALL-E 2 是一个可以根据英文描述来生成绘画的人工智能系统。该工具支持丰富的图像风格,如油画、卡通、漫画、现实主义、超现实主义、壁画等。它还可以模仿著名画家的风格,如达利、毕加索、梵高等。由 DALL-E 2 生成的图像质量非常高。我用下面的描述测试了这个工具:“一个快乐的人在海滩旁看日出的立体主义画作”。图 2 是 DALL-E 2 根据我的描述生成的图像之一。立体主义是毕加索推广的一种绘画风格。问问你的任何一个画家朋友,他/她都会说这确实是一幅立体主义风格的画。令人惊讶的是软件——它也许很复杂——能够模仿像毕加索、梵高、达利这样的大师。我强烈建议你体验一下它。这种体验将非常有趣,同时也体现了人工智能的威力。但请记住,像 ChatGPT 和 DALL-E 2 这样的工具也会带来很多问题,比如版权侵犯、学生的作业抄袭等。(LCTT 译注:本文的题图就是 DALL-E 3 生成的。)

介绍 scikit-learn
scikit-learn 是一个非常强大的机器学习 Python 库。它是一个采用 新 BSD 许可协议 (LCTT 译注:即三句版 BSD 许可证) 的自由开源软件。scikit-learn 提供了回归、分类、聚类和降维等当面的算法,如 支持向量机 (SVM)、随机森林、k-means 聚类等。
在下面关于 scikit-learn 的介绍中,我们将通过代码讨论支持向量机。支持向量机是机器学习中的一个重要的监督学习模型,可以用于分类和回归分析。支持向量机的发明人 Vladimir Vapnik 和 Alexey Chervonenkis。他们还一起提出了 VC 维 概念,这是一个评估模型分类能力的理论框架。
图 3 是使用支持向量机对数据进行分类的程序。第 1 行从 scikit-learn 导入 svm 模块。跟前面几篇中介绍的 python 库一样,scikit-learn 也可以通过 Anaconda Navigator 轻松安装。第 2 行定义了一个名为 X 的列表,其中包含训练数据。X 中的所有元素都是大小为 3 的列表。第 3 行定义了一个列表 y,其中包含列表 X 中数据的类别标签。在本例中,数据属于两个类别,标签只有 0 和 1 两种。但是使用该技术可以对多个类别的数据进行分类。第 4 行使用 svm 模块的 SVC() 方法生成一个支持向量分类器。第 5 行使用 svm 模块的 fit() 方法,根据给定的训练数据(本例中为数组 X 和 y)拟合 svm 分类器模型。最后,第 6 行和第 7 行基于该分类器进行预测。预测的结果也显示在图 3 中。可以看到,分类器能够正确区分我们提供的测试数据。
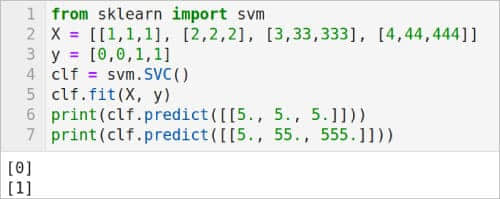
图 4 中的代码是一个使用 SVM 进行回归的例子。第 1 行次从 scikit-learn 导入 svm 模块。第 2 行定义了一个名为 X 的列表,其中包含训练数据。注意,X 中的所有元素都是大小为 2 的列表。第 3 行定义了一个列表 y,其中包含与列表 X 中的数据相关的值。第 4 行使用 svm 模块的 SVR() 方法生成支持向量回归模型。第 5 行使用 svm 模块的 fit() 方法,根据给定的训练数据(本例中为数 X 和 y)拟合 svm 回归模型。最后,第 6 行根据该 svm 回归模型进行预测。此预测的结果显示在图 4 中。除了 SVR() 之外,还有 LinearSVR() 和 NuSVR() 两种支持向量回归模型。将第 4 行替换为 regr = svm.LinearSVR() 和 regr = svm.NuSVR(),并执行代码来查看这些支持向量回归模型的效果。

现在让我们把注意力转到神经网络和 TensorFlow 上。但在下一篇讲无监督学习和聚类时,我们还会学习 scikit-learn 提供的其他方法。
神经网络和 TensorFlow
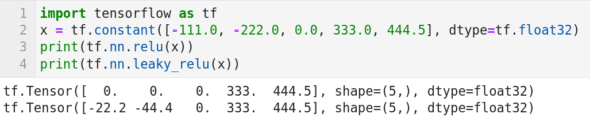
在上一篇中我们已经看到了 TensorFlow 的 nn 模块提供的 ReLU ( 整流线性单元 )和 Leaky ReLU 两个激活函数,下面再介绍两个其他激活函数。tf.nn.crelu() 是串联 ReLU 激活函数。tf.nn.elu() 是 指数线性单元 激活函数。我们将在后续用 TensorFlow 和 Keras 训练我们的第一个模型时用到其中一个激活函数。
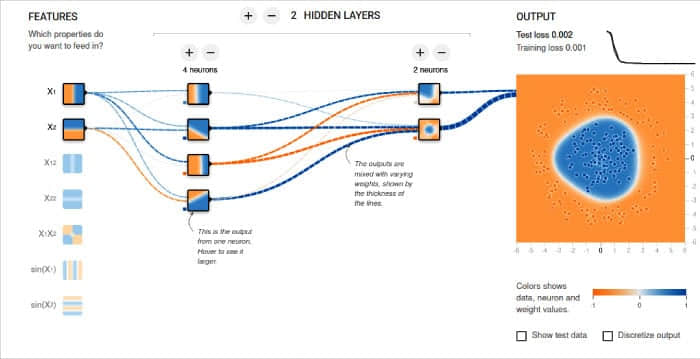
在开始训练模型之前,我想向你分享 TensorFlow 的提供的“神经网络实验场”工具。它通过可视化的方式帮助你理解神经网络的工作原理。你可以直观地向神经网络中添加神经元和隐藏层,然后训练该模型。你可以选择 Tanh、Sigmoid、Linear 和 ReLU 等激活函数。分类模型和回归模型都可以使用该工具进行分析。训练的效果以动画的形式显示。图 5 显示了一个示例神经网络和它的输出。你可以通过 https://playground.tensorflow.org 访问它。
训练第一个模型
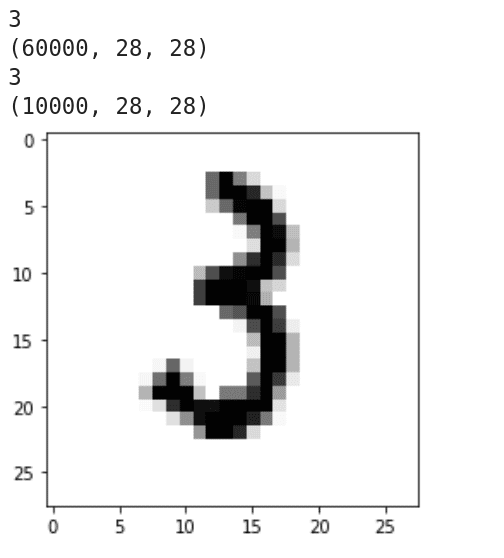
现在,我们使用 上一篇 提到的 MNIST 手写数字数据集来训练模型,然后使用手写数字图像对其进行测试。完整的程序 digital.py 相对较大,为了便于理解,我将程序拆分成几个部分来解释,并且添加了额外的行号。
import numpy as np
from tensorflow import keras, expand_dims
from tensorflow.keras import layers
num_classes = 10
input_shape = (28, 28, 1)
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data( )
第 1 行到第 3 行加载必要的包和模块。第 4 行将类别的数量定义为 10,因为我们试图对 0 到 9 进行分类。第 5 行将输入维度定义为 (28,28,1),这表明我们使用是 28 x 28 像素的灰度图像数据。第 6 行加载该数据集,并将其分为训练数据和测试数据。关于该数据集的更多信息可以参考 上一篇 的相关介绍。
x_train = x_train.astype("float32") / 255
x_test = x_test.astype("float32") / 255
x_train = np.expand_dims(x_train, 3)
x_test = np.expand_dims(x_test, 3)
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
第 7 行和第 8 行将图像像素值从 [0,255] 转换到 [0,1]。其中 astype() 方法用于将整数值类型转换为浮点值。第 9 行和第 10 行将数组 x_test 和 x_train 的维度从 (60000,28,28) 扩展为 (60000,28,28,1)。列表 y_train 和 y_test 包含从 0 到 9 的 10 个数字的标签。第 11 行和第 12 行将列表 y_train 和 y_test 转换为二进制类别矩阵。
try:
model = keras.models.load_model(“existing_model”)
except IOError:
model = keras.Sequential(
[
keras.Input(shape=input_shape),
layers.Conv2D(32, kernel_size=(3, 3), activation=”relu”),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(64, kernel_size=(3, 3), activation=”relu”),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Flatten( ),
layers.Dropout(0.5),
layers.Dense(num_classes, activation=”softmax”),
]
)
batch_size = 64
epochs = 25
model.compile(loss=”categorical_crossentropy”, optimizer=”adam”, metrics=[“accuracy”])
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)
model.save(“existing_model”)
训练模型是一个处理器密集和高内存消耗的操作,我们可不希望每次运行程序时都要重新训练一遍模型。因此,在第 13 行和第 14 行中,我们先尝试从 existing_model 目录加载模型。第一次执行此代码时,没有模型存在,因此会引发异常。第 16 到 21 行通过定义、训练和保存模型来处理这个异常。第 16 行代码(跨越多行)定义了模型的结构。这一行的参数决定了模型的行为。我们使用的是一个序列模型,它有一系列顺序连接的层,每一层都有一个输入张量和一个输出张量。我们将在下一篇文章中讨论这些定义模型的参数。在此之前,将这个神经网络看作一个黑箱就可以了。
第 17 行将批大小定义为 64,它决定每批计算的样本数量。第 18 行将 epoch 设置为 25,它决定了整个数据集将被学习算法处理的次数。第 19 行对模型的训练行为进行了配置。第 20 行根据给定的数据和参数训练模型。对这两行代码的详细解释将推迟到下一篇文章中。最后,第 21 行将训练好的模型保存到 existing_model 目录中。模型会以多个 .pb 文件的形式保存在该目录中。注意,第 16 到 21 行位于 except 块中。
print(model.summary( ))
score = model.evaluate(x_test, y_test, verbose=0)
print(“Test loss:”, score[0])
print(“Test accuracy:”, score[1])
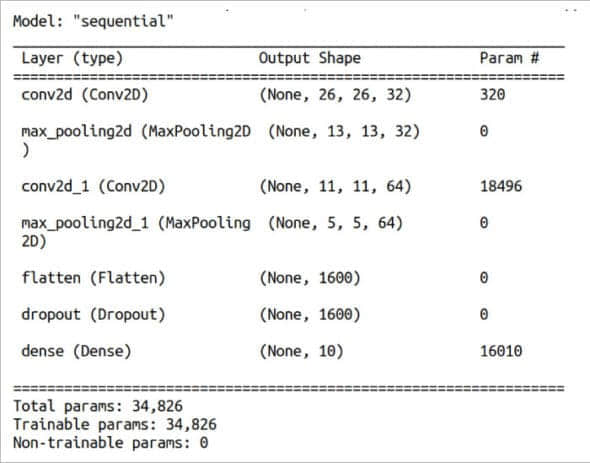
第 22 行打印我们训练的模型的摘要信息(见图 6)。回想一下,在加载数据集时将其分为了训练数据和测试数据。第 23 行使用测试数据来测试我们训练的模型的准确性。第 24 行和第 25 行打印测试的详细信息(见图 8)。
img = keras.utils.load_img("sample1.png").resize((28, 28)).convert('L')
img = keras.utils.img_to_array(img)
img = img.reshape((1, 28, 28, 1))
img = img.astype('float32')/255
score = model.predict(img)
print(score)
print("Number is", np.argmax(score))
print("Accuracy", np.max(score) * 100.0)
现在,是时候用实际数据来测试我们训练的模型了。我在纸上写了几个数字,并扫描了它们。图 7 是我用来测试模型的一个图像。第 26 行加载图像,然后将其大小调整为 28 x 28 像素,最后将其转换为灰度图像。第 27 到 29 行对图像进行必要的预处理,以便将它输入到我们训练好的模型中。第 30 行预测图像所属的类别。第 31 到 33 行打印该预测的详细信息。图 8 显示了程序 digital.py 的这部分输出。从图中可以看出,虽然图像被正确识别为 7,但置信度只有 23.77%。进一步,从图 8 中可以看到它被识别为 1 的置信度为 12.86%,被识别为 8 或 9 的置信度约为 11%。此外,该模型甚至在某些情况下会是分类错误。虽然我找不到导致性能低于标准的准确原因,但我认为相对较低的训练图像分辨率以及测试图像的质量可能是主要的影响因素。这虽然不是最好的模型,但我们现在有了第一个基于人工智能和机器学习原理的训练模型。希望在本系列的后续文章中,我们能构建出可以处理更困难任务的模型。

在本文介绍了 scikit-learn,在下一篇文章中我们还会继续用到它。然后介绍了一些加深对神经网络的理解的知识和工具。我们还使用 Keras 训练了第一个模型,并用这个模型进行预测。下一篇文章将继续探索神经网络和模型训练。我们还将了解 PyTorch,这是一个基于 Torch 库的机器学习框架。PyTorch 可以用于开发 计算机视觉 (CV) 和 自然语言处理 (NLP) 相关的应用程序。

致谢:感谢我的学生 Sreyas S. 在撰写本文过程中提出的创造性建议。
(题图:DA/c8e10cac-a5a5-4d53-b5eb-db06f448e60e)
作者:Deepu Benson 选题:lujun9972 译者:toknow-gh 校对:wxy