为什么排序的复杂度为 O(N log N)

基本上所有正而八经的算法教材都会解释像 快速排序 和 堆排序 这样的排序算法有多快,但并不需要复杂的数学就能证明你可以逐渐趋近的速度有多快。
关于标记的一个严肃说明:
大多数计算机专业的科学家使用大写字母 O 标记来指代“趋近,直到到达一个常数比例因子”,这与数学专业所指代的意义是有所区别的。这里我使用的大 O 标记的含义与计算机教材所指相同,但至少不会和其他数学符号混用。
基于比较的排序
先来看个特例,即每次比较两个值大小的算法(快速排序、堆排序,及其它通用排序算法)。这种思想后续可以扩展至所有排序算法。
一个简单的最差情况下的计数角度
假设有 4 个互不相等的数,且顺序随机,那么,可以通过只比较一对数字完成排序吗?显然不能,证明如下:根据定义,要对该数组排序,需要按照某种顺序重新排列数字。换句话说,你需要知道用哪种排列方式?有多少种可能的排列?第一个数字可以放在四个位置中的任意一个,第二个数字可以放在剩下三个位置中的任意一个,第三个数字可以放在剩下两个位置中的任意一个,最后一个数字只有剩下的一个位置可选。这样,共有 4×3×2×1=4!=24 种排列可供选择。通过一次比较大小,只能产生两种可能的结果。如果列出所有的排列,那么“从小到大”排序对应的可能是第 8 种排列,按“从大到小”排序对应的可能是第 24 种排列,但无法知道什么时候需要的是其它 22 种排列。
通过 2 次比较,可以得到 2×2=4 种可能的结果,这仍然不够。只要比较的次数少于 5(对应 2 5 = 32 种输出),就无法完成 4 个随机次序的数字的排序。如果 W(N) 是最差情况下对 N 个不同元素进行排序所需要的比较次数,那么,
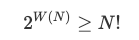
两边取以 2 为底的对数,得:
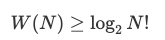
N! 的增长近似于 N<sup> N</sup> (参阅 Stirling 公式),那么,
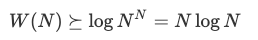
这就是最差情况下从输出计数的角度得出的 O(N log N) 上限。
从信息论角度的平均状态的例子
使用一些信息论知识,就可以从上面的讨论中得到一个更有力的结论。下面,使用排序算法作为信息传输的编码器:
- 任取一个数,比如 15
- 从 4 个数字的排列列表中查找第 15 种排列
- 对这种排列运行排序算法,记录所有的“大”、“小”比较结果
- 用二进制编码发送比较结果
- 接收端重新逐步执行发送端的排序算法,需要的话可以引用发送端的比较结果
- 现在接收端就可以知道发送端如何重新排列数字以按照需要排序,接收端可以对排列进行逆算,得到 4 个数字的初始顺序
- 接收端在排列表中检索发送端的原始排列,指出发送端发送的是 15
确实,这有点奇怪,但确实可以。这意味着排序算法遵循着与编码方案相同的定律,包括理论所证明的不存在通用的数据压缩算法。算法中每次比较发送 1 比特的比较结果编码数据,根据信息论,比较的次数至少是能表示所有数据的二进制位数。更技术语言点,平均所需的最小比较次数是输入数据的香农熵,以比特为单位。熵是衡量信息等不可预测量的数学度量。
包含 N 个元素的数组,元素次序随机且无偏时的熵最大,其值为 log<sub> 2</sub> N! 个比特。这证明 O(N log N) 是一个基于比较的对任意输入排序的最优平均值。
以上都是理论说法,那么实际的排序算法如何做比较的呢?下面是一个数组排序所需比较次数均值的图。我比较的是理论值与快速排序及 Ford-Johnson 合并插入排序 的表现。后者设计目的就是最小化比较次数(整体上没比快速排序快多少,因为生活中相对于最大限度减少比较次数,还有更重要的事情)。又因为 合并插入排序 是在 1959 年提出的,它一直在调整,以减少了一些比较次数,但图示说明,它基本上达到了最优状态。
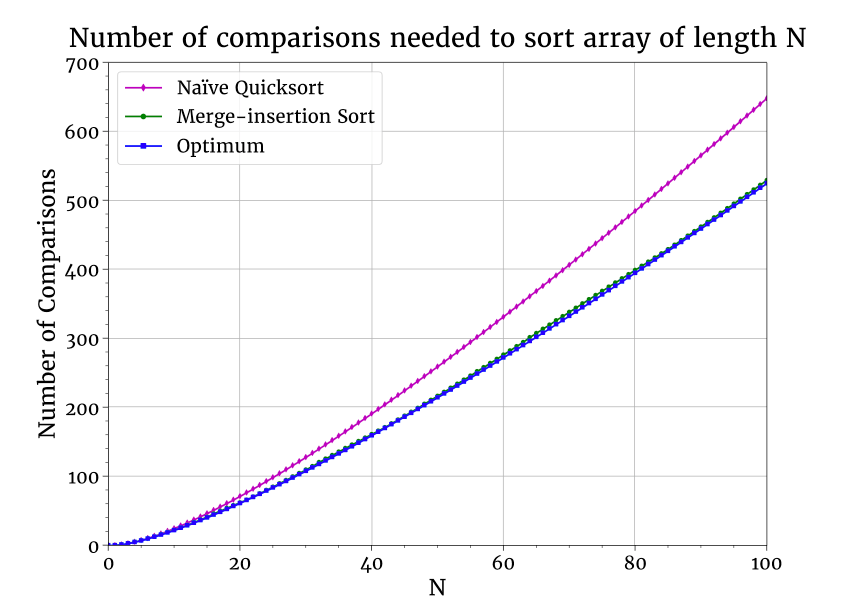
一点点理论导出这么实用的结论,这感觉真棒!
小结
证明了:
- 如果数组可以是任意顺序,在最坏情况下至少需要
O(N log N)次比较。 - 数组的平均比较次数最少是数组的熵,对随机输入而言,其值是
O(N log N)。
注意,第 2 个结论允许基于比较的算法优于 O(N log N),前提是输入是低熵的(换言之,是部分可预测的)。如果输入包含很多有序的子序列,那么合并排序的性能接近 O(N)。如果在确定一个位之前,其输入是有序的,插入排序性能接近 O(N)。在最差情况下,以上算法的性能表现都不超出 O(N log N)。
一般排序算法
基于比较的排序在实践中是个有趣的特例,但从理论上讲,计算机的 CMP 指令与其它指令相比,并没有什么特别之处。在下面两条的基础上,前面两种情形都可以扩展至任意排序算法:
- 大多数计算机指令有多于两个的输出,但输出的数量仍然是有限的。
- 一条指令有限的输出意味着一条指令只能处理有限的熵。
这给出了 O(N log N) 对应的指令下限。任何物理上可实现的计算机都只能在给定时间内执行有限数量的指令,所以算法的执行时间也有对应 O(N log N) 的下限。
什么是更快的算法?
一般意义上的 O(N log N) 下限,放在实践中来看,如果听人说到任何更快的算法,你要知道,它肯定以某种方式“作弊”了,其中肯定有圈套,即它不是一个可以处理任意大数组的通用排序算法。可能它是一个有用的算法,但最好看明白它字里行间隐含的东西。
一个广为人知的例子是 基数排序 算法,它经常被称为 O(N) 排序算法,但它只能处理所有数字都能放入 k 比特的情况,所以实际上它的性能是 O(kN)。
什么意思呢?假如你用的 8 位计算机,那么 8 个二进制位可以表示 2 8=256 个不同的数字,如果数组有上千个数字,那么其中必有重复。对有些应用而言这是可以的,但对有些应用就必须用 16 个二进制位来表示,16 个二进制位可以表示 2 16=65,536 个不同的数字。32 个二进制位可以表示 2 32=4,294,967,296 不同的数字。随着数组长度的增长,所需要的二进制位数也在增长。要表示 N 个不同的数字,需要 k ≥ log<sub> 2</sub> N 个二进制位。所以,只有允许数组中存在重复的数字时, O(kN) 才优于 O(N log N)。
一般意义上输入数据的 O(N log N) 的性能已经说明了全部问题。这个讨论不那么有趣因为很少需要在 32 位计算机上对几十亿整数进行排序,如果有谁的需求超出了 64 位计算机的极限,他一定没有告诉别人。
via: https://theartofmachinery.com/2019/01/05/sorting_is_nlogn.html
作者:Simon Arneaud 选题:lujun9972 译者:silentdawn-zz 校对:wxy
